Measuring GPS Speed Accuracy

 How do you know how accurate your GPS is? This question once again came up when I started looking into a "plug and play" GPS. Unfortunately, there's no simple answer to this question, so there will be a few posts looking at different aspects.

In search of the answer, the first thing to try is to use two GPS units right next to each other, and compare their speeds. Here is an example where I compared two Motion GPS units in a driving test:

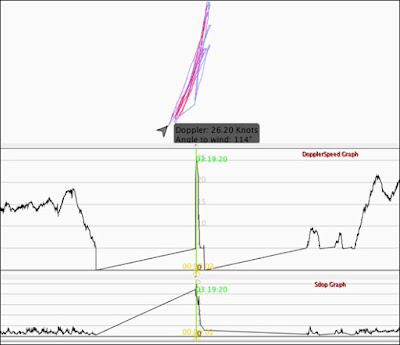
The speeds from one unit are drawn in red, the speeds from the other unit in blue. A lot of times, the speeds are so close that only one color is visible. Here's a zoom-in:

In the selected 10 second region (highlighted in yellow), the two GPS units gave almost identical speeds. For individual points, the speed differences were mostly below 0.1 knots; over the 10-second region, the average speeds were 13.482 and 13.486 knots. That's a rather small difference of 0.004 knots!

But the graph shows that this is not always the case. If we look at the region to the right, the observed differences get much larger:

Here, one GPS reports a 10-second average speed of 19.926 knots, while the other GPS reports 19.664 knots - a difference of 0.262 knots. In the context of a speed competition like the GPS Team Challenge, that's a pretty large difference. One interesting thing to note is that the speeds some times deviate significantly for more than a second; the dip in the red track in the picture above, for example, is about 3 seconds long. This is non-random error: in the 10 Hz data for the graph above, the "dip" extends over almost 30 points, which we'd expect to happen once every billion points by chance. We'll get back to this when we look at estimating the likely error of speed results.

The most straightforward way to compare different GPS units is to compare the results in different top speed categories. Here's a look at some of these, generated using the "Compare files" function in GPS Speedreader:

The table shows the speed results for the two devices, as well as the "two sigma" error estimates in the "+/-" column. The calculation of the result error estimates assumes that the errors are random, so that they would cancel each other out more and more when we look at more points: longer times or longer distances. This leads to higher error estimates for the 2 second results, roughly 2-fold lower estimates for the 10 second results, and very low estimates for the nautical mile (1852 m) and the 1 hour results. About 95 out of 100 times, we expect the "true" speed to be within the range defined by the +/- numbers. Most of the time, we expect the ranges of the two devices to overlap. Only about 1 in 10,000 results would be expect random errors to cause the results to be so different that the ranges do not overlap - which GPS Speedreader highlights by using a red background.

But the table shows that 5 of the 14 results are more different than expected. 5 out of 14, not one in ten thousand! There are three possible (and not mutually exclusive) explanations for this:

1. One (or both) of the GPS units is not working correctly.
2. The error in not random, so that the conclusions based on assuming random error are incorrect.
3. The single-point error estimates that the GPS gives are too optimistic.

Let's have one more look at the data, and this time, include a graph of the single-point error estimates:

We can see that the point error estimates in the regions where the curves diverge are larger, which is a good sign. But do they increase enough? And is the difference that we see due to one GPS being "wrong", or do both of them disagree, and the truth lies somewhere in the middle? To answer these questions, we need more data.

Fortunately, this was a driving test, so getting more data was easy: just put more GPS units on the dash board! So I added a few more: a couple of Locosys units (a GW-52 and a GW-60), a couple of u-blox prototypes that have been approved for use in the GPS Team challenge (a BN880 and a BN280, both Openlog-based), and my current u-blox Neo-M9/Openlog Artemis prototype. That makes a total of 7 GPS units: two with a Locosys Sirf-type GPS unit, and five with a u-blox based design. All units were set to log at 5 Hz for this drive. Here's an overview:

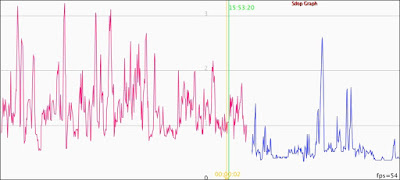
What is immediately apparent is that the error estimates differ a lot more than the speed estimates. In particular, the error estimates from the Locosys units, shown in purple and green, are much higher than the u-blox estimates, except when the car was stationary.

Here is a zoom-in picture:

Most of the GPS units are pretty close together for most of the time, but several units stick out a bit by showing larger and more frequent deviations. But just like in the first and second picture in this post, the details vary quite a bit between different sections of the drive.

So we're back at the question: how can we quantify the error of each of the units, using all the information in the tracks, instead of limiting us to just a few top speeds? 

Along the same lines, what can we learn about the point error estimates ("Speed Dilution of Precision", or SDoP, in Locosys parlance, and "speed accuracy", or sAcc, in u-blox parlance)?

I'll start looking at answers to these questions in my next post.

The Milk Jug Experiment

 My last post ended with this graph:

Before I tell you what I did to generate it, let's first look at the "why". Here's a short section from a recent windsurfing session that illustrates the problem:

I compared three different GPS units in this test. At the highlighted section, the three GPS units disagree from each other by roughly 0.5 knots for a few points in a row. Areas like this are easy to find in many GPS traces - but what causes them? The GPS units can be much more accurate that this, as stationary tests show, where typical errors are about 10-fold lower. 

One potential cause of the larger errors are short-term changes in the satellite signals received by the GPS; specifically, changes in the signal and/or noise for one or more satellites, and in which satellites the GPS uses to compute speed and position. So the experiment was to induce controlled changes, without moving the GPS, and see what effect they had on the observed error (the speed, since the GPS was stationary) and the error estimates given by the GPS.

To disturb the signal, I took a one gallon milk jug and filled it with water. I then moved it around the GPS and on top of the GPS, keeping a distance of at least a few centimeters, for about 30 seconds. I did that twice, with 30 second control periods where I kept the jug away before, in between, and after. The periods where I moved the jug around the GPS are highlighted in the first graph.

The speeds that were reported by the GPS because of the distorted satellite signal were around 0.5 knots multiple times, and near 0.8-0.9 knots a few times.  I was a little surprised to see such "speeds" just because the signal was partially blocked - after all, the GPS should still have been able to get a perfectly clean signal from most of the 20-25 satellites it was tracking. But apparently, having just a few signals removed or distorted is sufficient to cause errors in the range that we can often see in windsurf tracks.

Now I don't usually windsurf closely to people waving milk jugs, but it's just an example of a sudden change in the satellite signal cause by external factors. During windsurfing, that could be something as simple as changing the position of the arm that the GPS is on, or the body position, so that a different part of the sky is blocked by the arm or the body. The more things move around, the more likely that is to happen - and if you don't have the luxury of windsurfing at a flat spot like Lake George or La Franqui, chop might just do the moving for you.

In a similar experiment, I looked at what happened when moving the GPS up and down rapidly, and the results looked similar, even when looking at directional speeds (velN and velE). But my lovely wife pointed out that I could not really be sure that I was moving the GPS straight up and down, without side-to-side movement, so this experiment would need to be repeated in a more controlled fashion. For now, I'll just say that it is possible that rapid up-down movements of the GPS, which are typical when sailing in small to medium chop, might also have an effect on GPS accuracy.

One interesting question arises when comparing the results from different GPS units that are very close together, and technically identical (or very similar). They both should "see" the same distorted signal, so why would the not compute exactly the same result?

Rather than answering this question directly, or speculating about why this may not be the case, I'll show a graph from a stationary experiment where I had two identical units positioned very close to each other, with a clear view of the sky:

One interesting result shown in the table above is in the "sats" column, which shows how many satellites each unit tracked. Since the units were very close to each other and technically identical, it is reasonable to expect that they would use exactly the same satellites. But at the start of the highlighted region, one GPS used 17 satellites, while the other used 20 - that's a pretty substantial difference! Here is a graph of the satellites tracked by the two Motion units over a time of about 1000 seconds (starting a few minutes into the test, after both units showed the same number of satellites):

For large parts of the tests, the two GPS units differed in how many satellites they used - which means that blockage or distortions of one or a few satellites could affect the two units differently, thus possibly leading to comparatively large discrepancies in the results.

How does all this relate to speedsurfing, you might ask? The blocking experiment is an example of non-random noise in the data. If you look back at the first graph, you may notice that the error estimates increase much less than the speeds. This means that there are multiple regions where the error estimates are significantly lower than the observed errors for more than 10 points in a row - here is an example:

Statistically, we would expect to see some points where the speed is higher than the error estimates, but we should practically never see this many points where the error is larger than the error estimate in a row - if the error is random. But if the error is not random, then we can not use Gaussian error propagation, which makes collecting at high data rates entirely pointless.

Foil Against Noise

Let me start with a picture to make clear what this post is about:

It's about how a little bit of aluminum foil can help against RF noise from Raspberry Pies(the kind shown in the picture above - if other raspberry pies make you noisy, try the gluten free versions!).
The graph above shows the results from a stationary test, with measured speed on top, and accuracy estimates at the bottom. For the first 5 minutes of the test (the left, yellow half), I had covered the Raspberry Pi with a bit of aluminum foil; for the second half of the test, I put the Pi on top of the foil.

The results show that (a) the Pi generates a lot of RF noise that's picked up by the GPS and introduces error, and (b) that this RF noise can be blocked quite easily. For those of you who like numbers, here are the averages and maxima for this test (all numbers in knots):

For the numbers, I divided the second half of the test into two parts: a transition part, where the speeds and error estimates where high; and a "not blocked" part, when the numbers stabilized. Moving the Pi took just a few seconds, but the transition period lasted about 2 minutes. I'm not sure exactly what was going on there - perhaps the software in the GPS module needed a couple of minutes to figure out which satellites and/or noise filters to use. 

The numbers in the table above reflect what I had seen many times before in other data sets:

• At low error estimates (the "with foil" row), actual errors typically are below the error estimates.
• With higher error estimates, deviations larger than the error estimate can be observed more often.
• With poor data quality (high error estimates), the error becomes less random, with extended regions of larger error. This is illustrated by the high (false) speed over 2 seconds of more than 4 knots in the "Transition" period. In this region, 10 successive points had errors over 2 knots, about 2x to 5x as high as the error estimate. This would be extremely unlikely to occur randomly.

While the data shown are from a single test, the results are very reproducible. This is quite easy to do by simply hooking up the GPS to u-center, and opening a few graphs. Here's a screen shot from the part where the Pi was covered with foil:

Changes after uncovering the Pi where quite dramatic:

For a lot of the satellites (but not all of them), the observed signal-to-noise ratio dropped significantly, which reduced the accuracy of the speed calculations. So, if you want to use a Raspberry Pi to capture GPS data: cover your Pi!

Ducks Fly Fast

Ducks can fly - why can't I? It's not for lack of trying:

Maybe I need to flap harder? Or maybe I need to grow a pair .. of wings, that is. Probably won't happen.

The picture is from a session two days ago at Kalmus. After sailing back and forth for 9 hours the day before (I call that "distance sailing"), it was time to do something different - a bit of old school freestyle. I'll refrain from doing any freestyle as long as I have any excuse - "the water is cold" or "I did not sail much recently" being two of my favorites. So I still count the Duck Jibe as a freestyle trick. It's tricky to catch the sail after throwing it! Works better than trying to fly, though.

The crash in the picture above was harmless - perhaps all that flapping helped, after all. A little while later (and a little more tired), I had a better crash. If you've learned the Duck Jibe, maybe you remember the "Plank Walk": when your mast hits the water, and your gear suddenly stops, but you keep going ... straight off the nose of your board. That's pretty much what I did. Here's the GoPro footage:
That was fun! As a little bonus, I set my top speed of the day during my brief flight, according to my GPS:

I was three knots faster than in my second-fastest run! If you believe the GPS, that is. I really don't think that I was airborne for longer than 2 seconds - I would have flown about a 100 feet in that time! So let's look at the data more closely:

Here is the narrative to what happened:

• I slowed down a bit during the sail duck, from 22 knots to 18.5 knots
• When the mast hit the water, the board came to a sudden stop. Not so my body! Since my foot was still in the strap, the upper body did not just keep the speed, but actually accelerated from 18.5 to 26 knots within 0.4 seconds
• I hit the water shortly thereafter. As soon as my hand was deeper than about 2-4 inches, the GPS watch lost reception, since water absorbs the GPS signal. We can see that point #24220 is not the expected 0.2 seconds after the previous point, but rather 1.6 seconds. So 1.4 seconds worth of data are missing.
• GPS chips are made for cars, not for windsurfing. Cars often loose GPS reception, for example in tunnels or under bridges; but usually, they keep going at roughly the same speed and direction as before.  So the GPS chips go into "dead reckoning" mode, assuming that the "car" is still traveling at the same speed, and predicting the speed and new position.

Well, I may be many things, but a car I am not. I did stop when I hit the water. Speedsurfers traveling twice as fast as I did may bounce a few times before sinking, but I did not. So the GPS guessed wrong about how far and fast I traveled when I had no GPS reception. It corrected it's mistake very shortly thereafter: in point #24221, it adjusted the position by about 20 meters, roughly the same amount that it guessed wrong in the first place. The two points with large distances easy to see in the tracks:

For this particular file, only one of the three GPS speedsurfing programs gives the correct 2-second top speed. That is GPSResults, which refuses to use data points that have longer-than-expected time gaps. Both GPS Action Replay Pro and ka72.com use such data points, and therefore give an incorrect maximum 2-second speed that is "dead reckoning inflated" by about 3 knots.

Using accuracy estimates (SDoP filtering) to identify the "guessed wrong" data points could have worked, but would have required a threshold of 3.0 knots; the current threshold of 4.0 used by GPSResults would have let the bad points through. An "average SDoP" filter with a threshold of 1.5 that I had proposed earlier would have easily identified the bad points, and avoids the potential issues with invalidating larger stretches of data if single points are missing.

Now if I can only convince myself to duck jibe at the end of speed runs, maybe I'll finally get a 35 knot top speed...

Reader Comments about Filters

In response to my post about the "60 Knot New Speedrecord", a reader had a bunch of comments. I answered the first comment in the comment section of the original post, but he came back with a whole bunch more. Mathew wrote:

"Thanks for writing up a follow up. It should be pointed out that the acceleration filter shouldn't "per point" as highlighted in the follow-up... it should apply from last-good-point until the next point which doesn't breach the threshold. Also - and this example highlights it - once a filter has been breached in the middle of a run, the remainder of the run must be discarded [ most of the time ]. The problem here isn't that we dont understand what type of filtering is required - we already do know -> the problem is that the auto-filtering of the software analysis, doesn't match how humans do it. ie: if your data isn't clear, then then the data from that run shouldn't be used. [ Which is why we use two, three or four GPS's.... ] ... In the RealSpeed example, with 3ms-2 (5.5 kns-2) it takes about 3 seconds for the threshold to not be exceeded [ (20.8-4.5) / 5.5]. Since a new threshold is breached within 3 second window, the new window needs to be calculated... and so on. Thus about 7 seconds or so should be dropped.
A standard practice in all sciences, is to drop data that is completely bogus -> thus all "simple filtering" should be applied first, then apply SDoP filters last. [ Caveat: big-data analysis doesn't work this way generally speaking, as the algorithms are sometimes more accurate using bogus data. ] It would be useful to implement the filters accurately, then apply it to these examples vs. applying a simple SDoP filter.
... the point is -> SDoP/SDoS isn't a panacea - it doesn't replace simple physical constraints of the sport. Indeed humans naturally apply a few more physical constraints, ie: even though 3ms-2 is the threshold, it is completely unlikely to that you will sustain 1/3G acceleration for more than a few seconds simply because the drag component goes up very quickly [ vs terminal velocity of about 30m/s ]. "

This is pretty long, so let me just restate what I think he is saying in simple terms:

1. We know that acceleration in speedsurfing is limited to less than 5.5 knots/second
2. When looking at GPS tracks, that allows us to identify artifacts without any doubt. If the speed shoots up from 5 knots to 20 knots between 2 data points, we know something is wrong.
3. If software could implement this "physical constraint" in filters, that would allow the identification of artifacts without SDoP filters.
4. However, just throwing out single points where the acceleration is above the threshold is not good enough (as I had illustrated in response to his previous comment).

Before I go into a detailed analysis about these points, let me say that I mostly agree with Mathew. For example, the typical acceleration in speed runs is less than 2 knots per second. For example, check out one of Boro's recent traces where he got close to 40 knots:

Let's zoom in on the speed run in the middle:

I selected the region where the acceleration was highest, or close to it. Within about 4 seconds, he went from 31 knots to 36 knots - that's an acceleration of about 1.25 knots/second. So if we accept that this is a typical track, then a threshold of 5.5 knots/second seems rather safe. But is it?

Let's look at what the current default in the most accurate GPS analysis software is, GPSResults. For 5 Hz GPS data, the acceleration filter defaults to 8 m/second(squared) - that's 15.55 knot. That's about three times as high as what we said! Why does GPSResults not use the 3 m/s2 that Mathew suggests?

Well, theories are all nice and good, but it's always better to look at real data. I went through a test set of about 200 GPS files from GW-60 watches and GW-52 units to see how many of these files had points with an acceleration above 3 m/s2. The answer: 125 of 197. That's about 2 out of every 3 files! If we'd implement a filter with this threshold, it would remove good runs from the majority of files.

So what threshold would work? In the test set, the highest acceleration within the top five 10-second runs was 6.35 m/s2. If you're wondering what the data look like, here's a screen shot from my analysis software:

At the second point in the table, the doppler speed jumped from 25.562 knots to 28.03 knots - that's about 2.5 knots faster in 0.2 seconds! Looking at the track, the spike is quite obvious. It looks like random noise added on top of a much smaller real acceleration; in the next data points, the speed goes down again. Overall, though, this run looks good - there's no reason to discard it.

So even for this small set, we'd need a threshold close to 7. If we'd look at more test data, we'd probably find a few tracks with even higher numbers, so the threshold of 8.0 that GPSResults uses for 5 Hz data seems quite reasonable. Unfortunately, having to use a higher threshold throws off Mathew's argument a bit. 

The higher threshold is needed because the higher frequency data from the GW-60 and GW-52 devices has a lot more noise. That's not a problem - since we have a lot more data points, we can average out the noise. But trying to implement this in a filter will be quite a bit more complicated than it seems at first glance.

If we examine the current versions of 4 different programs to analyze GPS data (GPSResults, GPS Action Replay Pro, ka72.com, and RealSpeed), it appears that only one of the four has a reasonably implementation all filters that are known to work, and uses them by default when calculating speeds (I am talking about HDoP, SDoP, minimum number of satellites, and acceleration filters). Three out of the four programs are missing one or more of these filters, and/or require a separate manual step to apply them. This is for very straightforward filters: "if the value is above (or below) the threshold, mark the point as bad, and do not use it to calculate speeds". It would be a great improvement to see these simple known filters implemented in all four GPS analysis programs.

But even the most accurate program, GPSResults, currently fails to identify some artifacts that can occur when the data quality is marginal (but not obviously bad).  For this particular problem, better filters would be needed - for example filters that use average SDoP errors for short-term speed (or standard error estimates, which also consider all error estimates in a region, not just single points). For errors that result from "dead reckoning"-type overstatements, acceleration filters would not help at all - the very cause of the error is that the software inside the GPS tries to keep speed relative constant when the GPS signal is bad. So far, though, the level of interest in implementing better filters for such artifacts seems darn close to zero.

Let me finish with a comment on Mathew's pointers towards scientific and "big data" analysis. There are some interesting similarities between large-scale DNA sequence analysis and GPS analysis. I worked in large scale DNA sequencing at the beginning of the Human Genome Project (HGP), when the data were analyzed very much like GPS data are still analyzed for records: with some computer help, but also a lot of human checks at any problem regions. During the first years of the project, progress was very slow, and many scientists doubted that the project would finish on time. The first big breakthrough came when someone developed accurate "quality scores" - a measure how likely the sequence data points were to be correct, which is very similar to SDoP values. As soon as these quality scores were widely used, many analysis bottle necks were removed; the accuracy of the "final" results increased dramatically; and throughput jumped. The quality scores were one essential part that enabled further dramatic improvements which allowed the Human Genome Project to finish ahead of its deadline. Early on, I did a little bit of research to evaluate both the accuracy and the usefulness of the "SDoP-equivalent"; the results surprised me positively on both counts. 

In the early phases of the HGP, we did something that is very similar to the wearing of "2, 3, or 4" GPS units that Mathew mentioned - we'd also generate data several times over. We had lots of complex rules and highly educates scientists to check on any discrepancies; but in the end, we ended up with "finished" data that had orders of magnitude more errors that what late could be done completely automatically, using accuracy estimates (and proper filters and analysis algorithms).

So yes, I may be somewhat biased towards seeing the usefulness of accurate error estimates.

Overstating Speed by 4 Knots

This is a geeks only post. You've been warned.

I love my GW-60 GPS watch, and it has worked great for me. However, recent problems with accuracy that both Boro and Denis on our team had seen made me wonder how often such issues arise. I had never seen them in my data, and I often looked closely enough that I would discover them. But many speedsurfers just quickly analyze the data to get their speeds, and upload those speeds, trusting whatever the software tells them.

So I went on a little fishing expedition on ka72.com. I searched for downloadable GPS sessions from May 15, 2017 onwards, and downloaded data files that were from GW-60 watches. Then, I looked at the tracks in detail in GPS Action Replay Pro and GPSResults, searching for examples where the 2 second speed was overstated.

After checking 15 files, I found one with a problem:  the top speed was just a few seconds of 25-knot speeds, in the middle of what looked like a longer swim. That's not how top speeds are reached! Sure enough, the GPS analysis software came to different results: Ka72.com and GPSResults gave a top speed of 25.3 knots, but GPSResults gave only 21.37 knots - 4 knots less! Let's look at the data:

This windsurfer had set up his watch to record only if the minimum speed exceeded 5 knots. The middle graph shows the speed: it was below 5 knots for about 4 minutes, with a few seconds where he supposedly sailed a lot faster than during the test of his session. The tracks on top show that this was at the very end of a run, after turning around - very suspicious! The accuracy graph at the bottom confirms the suspicions: the watch new that it did not have good data, and gave the data near the spike a much higher error estimate than the test of the track. Which, by the way, is why GPSResults did not include this region when it looked for top speeds.

Here are the data points in this region:

All data points in this regions have +- numbers between 3.2 and 4.957 - in other words, they are junk and should be ignored. For this screen shot, I forced GPSResults to behave badly by turning the filters off. The two other analysis programs, GPS Action Replay and ka72.com, always behave badly with data like this - they do not have SDoP filters.

In both this and the previous example of speed artifacts, the errors occurred during prolonged times where the windsurfer apparently was in the water, probably swimming, trying to waterstart, or resting. In such situations, GPS watches are more prone to artifacts because of where they are typically worn: on the wrist (instead of on the upper arm or helmet like other GPS devices). That means the watch will be under water much more than a GT-31 or GW-52 GPS, not getting any GPS reception because water absorbs the GPS signal. But at times, the watch may be close to or just above the water, and get a signal for a short time. At that point, the GPS chip has to re-acquire the satellites, and calculate the current position from scratch - which can introduce big errors, especially if the reception is marginal. In the tracks and the non-doppler speed graphs, there are often big jumps and spikes when this happens. Usually, that's not a problem with doppler speeds (which is exactly why we use doppler speeds for GPS speedsurfing!): single speed spikes from position adjustments just disappear in the doppler speeds. But when swimming with the watch close to the surface, we sometime see multiple spikes in the speed graphs. When that happens, the error can "go through" to the calculated doppler speeds, which is what we see in the graphs above.

Many speedsurfers may never see issues like this one because they sail in shallow locations, nail their jibes, and/or waterstart quickly very time they crash. But if you have a session where you spend a considerable amount of time in the water, then the chances of errors like the one described here are significant. Sometimes, it's obvious - Denis knew he had not set a new world record. Other times, it's not; in the example above, the 2 second speed seems reasonably close to the 10 second speeds, at least at first glance, so the result was posted to the GPS Team Challenge. In this case, it did not affect anything; but similar problems could happen during faster sessions that count for the monthly ranking.

While this particular problem here may be specific to GPS watches, and maybe even the GW-60 watch, I have seen similar artifacts in GPS data from all kinds of devices, including the long-time "gold standard" GT-31. Typically, it's easy to recognize such problems if you look at the your GPS traces, and examine your doppler speed graphs for the top speeds. In GPS Action Replay, I also find the "SDoP" graph quite useful to identify problem areas. I don't find GPSResults quite as intuitive, but then, GPSResults does a much better job at filtering out problem areas automatically, so the results are more likely to be accurate in the first place. Hopefully, we'll also see similar automatic filtering soon on ka72.com and in GPS Action Replay Pro.

60 Knots - A New Speedrecord?

Short answer: no. Before I get to the long answer, let me warn you: this is another one of my geeky posts. I reckon it may be of interest to about 5 or 10 windsurfers in the whole world! You've been warned.

This all started when our "United Speedsailors of America" team member Denis posted results from a recent session. He had uploaded his results to ka72.com, and it showed that he had reached 2 second speed of 59.88 knots:

Denis does around 40 knots on a regular basis, so he is wicked fast. But he also knew that he definitely had not broken the world record for 2 second top speed (55.23 knots by Antoine Albeau on the Lüderitz Speed Channel). Even the ka72 results hinted in that direction: his best 10 second speed was just 30.1 knots.
Furthermore, Denis often sails with Boro, who just recently had his own problems with GPS accuracy,  so he was very skeptical about what his watch tried to tell him. He had also worn his old trusted GT-31 GPS unit, and that had reported a top speed of only around 30 knots.
World-famous speed surfer and GPS guru Roo (yes, he is from Australia!) immediately looked at the tracks, noticed that during the time of the supposed record speeds the "sat count dropped to 6/7", and came to the conclusion that due to "the surrounding mountains the sats that were just above the horizon produced poor signals which caused the anomoly".

Well, this seems to make sense - Denis and Boro are windsurfing on a mountain lake, so the mountains around it must be too high! Since almost everyone else is windsurfing in flat terrain, maybe we can just ignore their problems? That's simple! Simple is great! Right?

Not so fast, cowboy! Sure, there are 10,000 ft (3,000 m) mountains around Washoe Lake. But the lake itself is at 5000 ft elevation, measures 2 x 4 km, and is in a valley that extends more than 10 km from each end of the lake. So a lot of the sky and the GPS satellites will be visible. So let's look at the tracks:

The doppler speed graph from his GW-60 watch is shown on the top in red; for comparison, the GT-31 data are shown in blue at the bottom. The GW-60 data show 3 spikes: 2 above 50 knots, and one above 70 knots! Before we jump to any hasty conclusions, let's zoom in on the largest spike:

We can see that the blue (GT-31) graph shows a speed close to zero around the time of the spike. In other words, Denis was most likely in the water at that time. There are few things that kill GPS reception as well as a few inches of water! We can also bet that Denis wore his watch on his wrist, and the GT-31 on his upper arm, so at times, the watch will have been deeper under water. Sure, the watch should not show a spike like this .. but I have seen similar spikes in GT-31 data in the past (and do not usually see them in GW-60 data, even when I fall a lot). As Forest Gump said: "It happens".

But let's not stop there - let's look at the actual data points:

Pay attention to the "+/-" column, which shows error estimates for the speed (also called "SDoP", for "Speed Dilution of Precision"). The SDoP values start at around 2, but then quickly jump up to 4.957, which is where they stay for a while. At the first line of the highlighted area, we can also notice that the time between data points jumped from 0.2 seconds to 16.6 seconds - for more than 16 seconds, the GPS did not have enough reception to calculate speed. Denis, where was your hand?

If you wondered why the +/- numbers never got higher than 4.957, give yourself a geek gold star! That's simply because the SDoP numbers are stored as a single byte in the .sbp files, and the highest number possible corresponds to 4.957 knots. In plain English, an SDoP of 4 or higher indicates complete junk.

So, the watch actually knows that these data points are junk! Any analysis software should now, too! As guru Roo correctlu pointed out, GPSResults completely ignores the problematic data points, and gives top speed results that are practically identical to the results from the GT-31 unit. GPSResults has an SDoP filter, and by default refuses to include any regions with SDoP values above 3.0 (for 5 Hz data). The big question remains: what about other software?

Many Australian speed surfers analyze their results on ka72.com, and Denis did. However, it appears that ka72.com either does not use SDoP filters, or does not use them correctly. If we assume that Denis' problem had more to do with putting the watch under water than with being surrounded by mountains (which was not a problem when he was not swimming), then this problem might affect many other speed surfers, and needs to be addressed (there's also a problem with the alpha 500 numbers being wrong for this track).

Now, how about my favorite GPS analysis software, GPS Action Replay Pro (GPSAR, which I used to create all the screen shots above)? Unfortunately, the results are not pretty:

GPSAR calculates a top speed of 64.55 knots! Based on the settings shown in the speed dialog, GPSAR does not have any SDoP filtering at all, and thus arrives at incorrect results.

So, here's the bottom line:

• Accuracy estimates are fantastic to automatically identify bad data can lead to very large over-estimates - even fake "world records"
• ka72.com and GPS Action Replay Pro do not appear to have functioning SDoP filters at this point in time; any data analyzed with either software should be carefully checked!
• GPSResults has SDoP filters that can correctly identify artifacts such as the ones described here; however, as I have shown in a previous blog entry, the default settings may not be adequate to catch smaller errors, which can overstate speeds by a knot or two

--

As mentioned above, Denis's data files are available on ka72.com. I also made zip files with the data from my previous post about GW-60 accuracy for Boro's data and for the 6-GPS test drive.

--
Added May 28, 2017:
In a comment to this post made today, Mathew made the bold statement "You dont need SDoP - just have a sensible acceleration filter". Well, acceleration filter can indeed be helpful to identify some problems, but they can not identify all problems that SDoP filters can find. The program GPS Action Replay does have an acceleration filter, but using it (which is an extra step that most users won't do) does not fix the problem. Applying a 3 m/s2 acceleration filter in the current version of GPSAction Replay (5.23) removed 801 points from Denis' track:

But afterwards, the speed table still shows a top 2 second speed that is 17 knots to high:

That's a little better than the 64.55 knots before the filter, but still wrong. Perhaps this is a bug in GPS Action Replay that could be fixed - but acceleration filters can, by definition, only identify some artifacts: those with too much acceleration. In case of artifacts that remain high for a few seconds, acceleration filters will fail. Here's an example, using RealSpeed and the problem trace I described in my next post:

Here, the speed increases from less than 1 knot to 20.5 knots in 0.2 seconds, and then to 24.7 knots. After that, the speed remains around 23-25 knots for more than 2 seconds. The acceleration filter identifies the first 2 points, and also a few points at the end of the artifact (shown in red); but the points in the middle have low acceleration and look fine to the filter, which is why they are shown in green. Even after applying the acceleration filter, this data set still gives a 2 second "top speed" that is from an artifact, and 4 knots higher than the real top speed in this track. But the SDoP values in this region, which are all above 3, make it very clear that the data cannot be trusted and should be discarded.

Another example of errors which acceleration filters cannot catch, but SDoP filter can, are the more subtle 1-2 knot errors that can result from using an underhand grip in speed runs, with the watch facing downward and the lower arm blocking the GPS signal. It remains to be seen, however, what the best thresholds and implementation details for SDoP filters are that can catch such artifacts, without throwing out "good" data where just a single data point has higher-than-usual error values. That requires looking at a bunch of GPS files in detail to see how to separate the good from the bad, and will take a while.

The Fastest Way To Get Faster

Some people who saw me driving around today looked at me in a funny way. Was it because I had my arm out of the window in 54ºF (12ºC)? Or maybe because I had 6 GPS units strapped to my arm?

In case you're wondering: I was wearing two yellow GW-52 units on top; two GW-60 PGS watches on the wrist, one facing up and one facing down; and a GT-31 plus a third GW-52 at the bottom.

As fascinated as I am with GPS speedsurfing, even I need a good reason to strap more than $1000 in GPS devices on my arm and go for a drive. I had one! I wanted to reproduce what Boro had accomplished recently. Boro wanted to start using his GW-60 watch, and compared it to his trusty old GT-31 GPS units. He got substantially higher speeds from the GW-60 watch:

• 2 seconds:
  37.99 knots GW-60, 36.29 knots GT-31
• 5x10 seconds:
  33.71 knots GW-60, 33.20 knots GT-31

That's 1.7 knots more for 2 seconds! It takes me (and others) years to improve my speed by that much! In many other tests, the speed of the watch had been much closer to the speed of other GPS units - was his watch broken, or was there another cause?

Looking at Boro's GPS files, it was obvious that his speed data had unusually high error margins of +- 1 to 2 knots; that's at least 2 times higher than usually, and about 5 times higher than what can be achieved with good GPS satellite reception. The error margins were about 2x higher when he was going the direction of his speed runs than when he was sailing back.

The first suspicion was that he was using an undergrip, with his watch hand closer to the mast, on his speed runs, and Boro quickly confirmed that this had indeed been the case. The human body is a very good absorber of GPS signals, and the GPS gurus had been very concerned about this very scenario - watches faces down towards the water, with an arm between them and the GPS satellites. I quickly did a little test walk with a couple of GW-60 watches on my wrist, one facing up and one down, and was able to reproduce the roughly 2-fold increase in error estimates if the watch is facing down.

But could such an increase in speed errors cause the observed difference in speed? There are some theoretical arguments against that: if the error is random, and we collect data at 5 Hz, we get 10 data points for 2 seconds, and 50 for 10 second runs. Average error should sometimes go up, sometimes go down, so that the total error should go down the more points we have. With 10 points, we'd expect the error to go down about 3-fold; with 50 points, about 7-fold. With data like Boro's that have about 1.5 knots error estimates, the expected error for 2 seconds is just 0.5 knots; for 10 seconds, it's closer to 0.2 knots; for 5x10 seconds, even lower.

So, something just is not right here. Instead of boring you to death with more theory and statistics, let's get back to my little drive. The idea was simple: let's just see what actually happens if we go for a drive with a bunch of GPS units, some facing up towards the satellite, some facing down. Somewhere in the middle of the drive, turn the arm around by 180 degrees and see what happens! And, most importantly - what's the effect on the top speed?

Let's start with a look at the speeds:

This is about 15 minutes worth of data from 6 GPS units - a bit too much information to see much. I deleted a few data points in the middle, where I turned my arm around. I also split the tracks into 2 segments for each device, before and after I turned the arm. So each device was pointing up for one segment, and down for the other.

Let's jump straight to the 2 second speed results from the first segment:

Four units show top speeds close to 28 knots: all the units that were facing up, and the GT-31. But the GW-60 watch and the GW-52 unit that were facing down show speeds that are almost one respectively 2 knots higher! Let's look at the data in detail:

The top graph shows the doppler speed, the bottom graph shows the error estimates. What stands out is:

• Two speed curves are substantially higher than the others: the black (GW-52 #3) and the red (GW-60 #2). 
• The same two GPS units have error estimates in this region that are about 2x higher than the other units,
• The observed error is not random. Both the red and black speed curves stay about 2 knots above the other curves for 8-10 seconds (40-50 data points). If the error would be completely random, this would be extremely unlikely to happen by chance; winning the jackpot in a lottery is more likely.

I can only speculate why the error becomes non-random at high SDOP values, but there's a likely guess: when the signal quality gets too low, the firmware starts to rely more on "dead reckoning". GPS chips sometimes use dead reckoning when no GPS signal is available, for example in tunnels. A sensible firmware implementation would start using increasing amounts of dead reckoning as the signal quality decreases, rather than a single "all-or-nothing" threshold. There are several indications that something like dead reckoning is causing the observed error characteristics, but that probably deserves another post.

Another question that arose was whether the problems are specific to the GW-60 watch, since it apparently has a GPS antenna that is smaller than the antenna in the GT-31, and thus possibly inferior. Let's look at the error estimate graphs from the "up" and "down" segments to get an idea. I color-coded the graphs so that blue indicates "up", and red indicates "down". Here's the GW-60 watch:

The SDOP values roughly doubled when I turned my arm so that the GPS was facing down. Here's the same graph for a GW-52:

Pretty similar, again with a marked increase when the GPS unit was faces down under my lower arm. Finally, let's look at the GT-31:

The GT-31 was facing down during the first segment, and up in the second segment. Again, we see much better data accuracy with the GPS facing up towards the satellites. Note that I sometimes had to take my hand into the car to turn, and that I may not always have had the arm oriented perfectly up or down, but the overall trend is clear: all three devices show the same trend towards much degraded accuracy of the GPS is worn facing to the ground.

Here are some conclusions and suggestions from this analysis (some of these points just re-iterate what others have stated many time before):

• When using a GPS watch, make sure that the watch is facing up during your speed runs! If you use an undergrip on your front hand, wear the watch on the inside or (even better) on your back hand. Or get an armband extended and wear the watch around your bizeps - it will get better reception there. For the best GPS reception and the most accurate data, consider mounting it on your helmet (if you wear one).
• The GPS analysis software may need to be modified to deal with poor quality data better. For example, the default SDOP cutoff of 3.0 that GPSResults uses for 5 Hz data seems too high, as the example above and Boro's initial experience show.
• While the examples I have shown here focus on speed over-estimates, it's just as possible that the error goes the other direction, and the speed is under-estimated. Here's an example:

The red track is from a downward-facing watch, and the speed happens to be several knots too low just around the maximum speed for this region. So wearing the watch facing downward during speed runs may not just be the quickest way to pick up a knot or two - it may also be the quickest way to loose a knot. So - keep it up!